When do two ellipses overlap/intersect
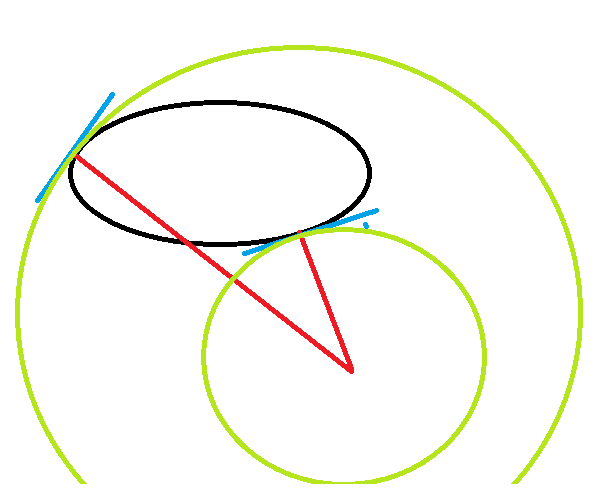
See also here A general rotated ellipse is \(f(x,y) = a x^2+2 b x y+c y^2+d x+e y - 1\) = X.M.X Nearest point (x,y).(df/dx, df/dy) = 0. Let this point be (X1,Y1) and (X2,Y2). X1^2+Y1^2 = R1^2 Therefore a circle radius between R1 and R2 intersects. A circle of radius >R1 overlaps. We need to find the relationship between roots of two quadratic simultaneous equations and their coefficients. It intersects a circle of radius 1/C if (x1^2+y1^2-1/C)(x2^2+y2^1-1/C)<0 or: (9*e^4+18*d^2*e^2-24*c*e^2+24*a*e^2-96*b*d*e+9*d^4+24*c*d^2-24*a*d^2+16*c^2-32*a*c+64*b^2+16*a^2)* C^2 + (-6*a*e^4+12*b*d*e^3-6*c*d^2*e^2-6*a*d^2*e^2+8*a*c*e^2-16*b^2*e^2-8*a^2*e^2+12*b*d^3*e+16*b*c*d*e+16*a*b*d*e-6*c*d^4-8*c^2*d^2+8*a*c*d^2-16*b^2*d^2)* C +a^2*e^4-4*a*b*d*e^3+2*a*c*d^2*e^2+4*b^2*d^2*e^2-4*b*c*d^3*e+c^2*d^4 < 0 (which is a 6th degree polynomial) To convert this to the case where we have two ellipses we need to transform: a*x^2+2*b*x*y+c*y^...